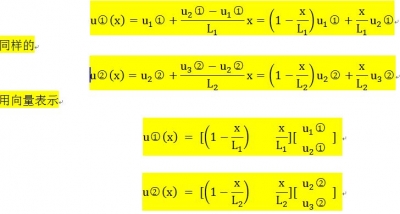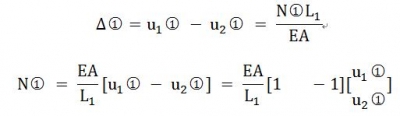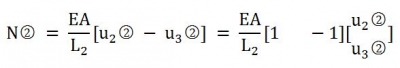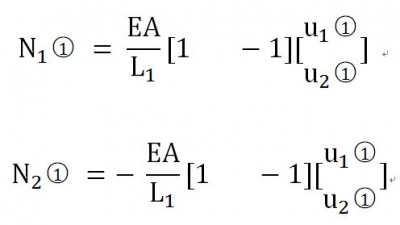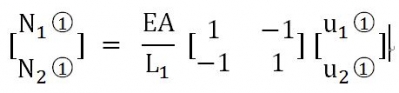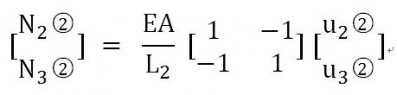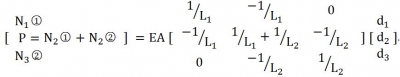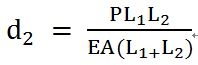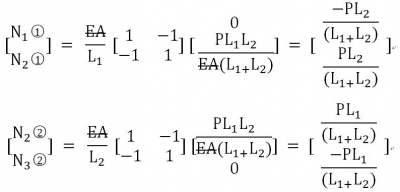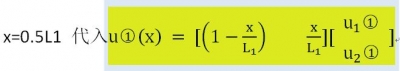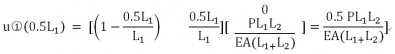��־
����Ԫ�W(xu��)��(x��)֮· ֮һ
��� 2 |
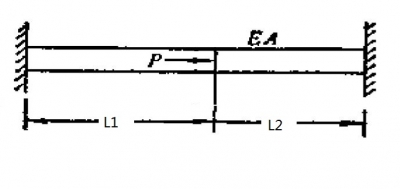
���O(sh��)һ����ֱ�U������ģ��E,������eA,���L(zh��ng)��2L�ɶ˹̶�,�������gλ��ʩ��һ���ҵ��d��P,����ֱ�U��(n��i)��(y��ng)��,��
�������W(xu��)�ⷨ�����O(sh��)P�������c(di��n)�l(f��)����һСλ��X
����ꮅ,��
����Ԫ�ⷨ˼·��
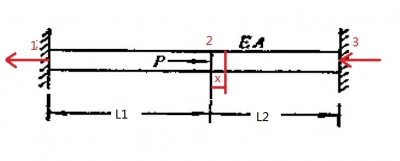
��ֱ�U���֞�2��(g��)��Ԫ ,�����@�B��(g��)�xɢ��Ԫ�ĽM�ρ�(l��i)�ƽ��B�m(x��)�wֱ�U���O(sh��)��Ԫ��̖(h��o)
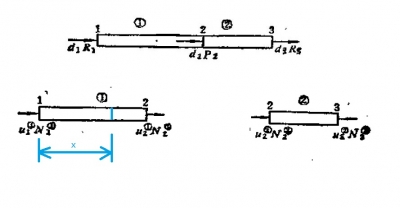
,�����@�B��(g��)�xɢ��Ԫ�ĽM�ρ�(l��i)�ƽ��B�m(x��)�wֱ�U���O(sh��)��Ԫ��̖(h��o) ,���Y(ji��)�c(di��n)��̖(h��o)1,��2��3,����Ԫ���S��λ���c�S���(n��i)�����ψD u��ʾ�Y(ji��)�c(di��n)λ�� N��ʾ�Y(ji��)�c(di��n)��(n��i)��,��
,���Y(ji��)�c(di��n)��̖(h��o)1,��2��3,����Ԫ���S��λ���c�S���(n��i)�����ψD u��ʾ�Y(ji��)�c(di��n)λ�� N��ʾ�Y(ji��)�c(di��n)��(n��i)��,��
���O(sh��)x���Ԫ 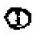 ��(n��i)����һ�c(di��n)�tλ�Ʊ��_(d��)ʽ�飨���µ�λ�Ʊ��_(d��)ʽ����O(sh��)�ģ��䌍(sh��)��������Ԫ�еĆ�Ԫ�κ���(sh��)��
��(n��i)����һ�c(di��n)�tλ�Ʊ��_(d��)ʽ�飨���µ�λ�Ʊ��_(d��)ʽ����O(sh��)�ģ��䌍(sh��)��������Ԫ�еĆ�Ԫ�κ���(sh��)��
����(j��)���˶���,����(du��)�چ�Ԫ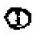 ,�����S�������l(f��)��λ��
,�����S�������l(f��)���
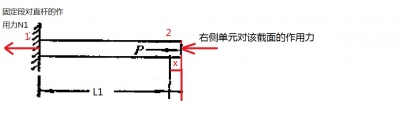
��(du��)��Ԫ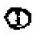 �����������ó��Y(ji��)�c(di��n)��������r
�����������ó��Y(ji��)�c(di��n)��������r
��������Ԫ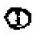 �ĽY(ji��)�c(di��n)�������_(d��)ʽ���ɾ�ꇽY(ji��)��(g��u)
�ĽY(ji��)�c(di��n)�������_(d��)ʽ���ɾ�ꇽY(ji��)��(g��u)
ͬ�ӵķ�ʽᘌ�(du��)��Ԫ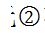 ,����ô��Ԫ2 �ĽY(ji��)�c(di��n)�������_(d��)ʽ�ľ�ꇽY(ji��)��(g��u)��
,����ô��Ԫ2 �ĽY(ji��)�c(di��n)�������_(d��)ʽ�ľ�ꇽY(ji��)��(g��u)��
���Y(ji��)�c(di��n)����B�m(x��)�l�� 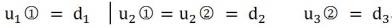
��Ԫ �Ą��Ⱦ�ꇷ��̿��ԽM�ϵ�������ʽ�����w���Ⱦ�ꇷ��̣�
�Ą��Ⱦ�ꇷ��̿��ԽM�ϵ�������ʽ�����w���Ⱦ�ꇷ��̣�
�Ɍ���������ʽ P = Kd K �������� �Y(ji��)��(g��u)�����Ⱦ�� d �������� �Y(ji��)��(g��u)�Y(ji��)�c(di��n)λ������ P �������� �Y(ji��)��(g��u)�Y(ji��)�c(di��n)�d������
߅��l�� d1=d3 =0 �������
�������Ԫ��(n��i)������
���F(xi��n)��λ���҂����](m��i)��ʹ���Sɫ�������ֵĹ�ʽ,������ʲô�����أ�Ŀǰ�҂��ܵõ����Ǹ��Y(ji��)�c(di��n)��λ��,�����c(di��n)������,���Լ��U�ă�(n��i)������(n��i)��(y��ng)�����˕r(sh��)��?y��n)邀(g��)��Ԫ��(n��i)���đ�(y��ng)��̎̎��ȣ����������Æ�Ԫ��(n��i)����̎��λ����,���Ǿ͵�ʹ���Sɫ���ֵă�(n��i)����,�������Ԫ ���gλ�ðl(f��)����λ���Ƕ���
���gλ�ðl(f��)����λ���Ƕ���
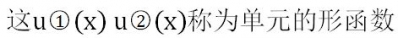 �������H����������Ԫ�ă�(n��i)��ֵ����(sh��),�����ц�Ԫ��(n��i)����һ�c(di��n)��λ���ýY(ji��)�c(di��n)λ�Ʊ�ʾ,�����ҿ�����ә�(qu��n)�������еļә�(qu��n)����(sh��),������̎�����d��,�����ֲ�����Ч��Y(ji��)�c(di��n)�ϵļ����������أ���������ڵȅ���Ԫ������(bi��o)׃�Q,��
�������H����������Ԫ�ă�(n��i)��ֵ����(sh��),�����ц�Ԫ��(n��i)����һ�c(di��n)��λ���ýY(ji��)�c(di��n)λ�Ʊ�ʾ,�����ҿ�����ә�(qu��n)�������еļә�(qu��n)����(sh��),������̎�����d��,�����ֲ�����Ч��Y(ji��)�c(di��n)�ϵļ����������أ���������ڵȅ���Ԫ������(bi��o)׃�Q,��