|
發(fā)布時(shí)間: 2016-10-27 09:21
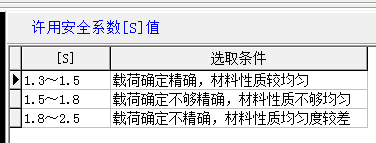
正文摘要:大家討論下,,在做很多設(shè)計(jì)時(shí)都要取個(gè)安全系數(shù),那么安全系數(shù)值的大小究竟是怎么確定的(即使是經(jīng)驗(yàn)獲得),? |
| 一般是2~3 |
| 我一般設(shè)計(jì)時(shí)安全系數(shù)選擇2,,校核時(shí)把安全系數(shù)降低到1.5再看看是否可以 |
|
首先得查機(jī)械手冊(cè),然后和實(shí)際經(jīng)驗(yàn)想對(duì)比,。 |
陳小困 發(fā)表于 2016-10-27 11:08 估計(jì)不到 5 |
|
回答這個(gè)問題前,,先要費(fèi)點(diǎn)口舌說說為什么要有安全系數(shù)以及安全系數(shù)的本質(zhì)是什么。 從純而又純的理論出發(fā),,只要負(fù)載小于構(gòu)件的承載能力,,就不會(huì)有破壞發(fā)生,如同0.999999……<1,,永遠(yuǎn)不會(huì)有問題,。然而,實(shí)際情況從來不是也永遠(yuǎn)不會(huì)是純而又純的理論所描述的那樣簡(jiǎn)單,。材料的性能,、構(gòu)件的尺寸必然會(huì)有這樣那樣的偏差,實(shí)際載荷也會(huì)有這樣那樣的變化,。對(duì)這些偏差和變化的描述,,運(yùn)用到統(tǒng)計(jì)技術(shù),于是有了統(tǒng)計(jì)特征——均值,、方差……,。 在做設(shè)計(jì)計(jì)算時(shí),計(jì)算公式能處理的只能是確定的具體數(shù)字,,于是采用均值是個(gè)現(xiàn)實(shí)并且合理的選擇,。當(dāng)選擇設(shè)計(jì)承載能力大于給定負(fù)荷時(shí),后一個(gè)問題就會(huì)冒出來——構(gòu)件的的承載能力是在一個(gè)范圍內(nèi)分布的,,實(shí)際的載荷也在一個(gè)范圍內(nèi)分布,,這兩個(gè)分布一旦有重合區(qū)出現(xiàn),就有了發(fā)生破壞的概率,。我們做的只是將兩者的均值錯(cuò)開,,而這兩者的分布會(huì)在何種程度上重合? 安全系數(shù)由此產(chǎn)生:將根據(jù)均值設(shè)計(jì)的承載能力以一定的倍數(shù)與給定的負(fù)荷均值錯(cuò)開,,使兩個(gè)分布的疊加區(qū)小到可以接受,。這是一種簡(jiǎn)單有效的處理方法,,雖然顯得有些粗糙,不太講理,。 在數(shù)學(xué)層面上考慮這個(gè)問題,,安全系數(shù)應(yīng)該這樣得到:給定的載荷分布和承載能力分布條件下,安全系數(shù)給出了兩者均值的偏距,,也就確定了分布的疊加范圍即破壞發(fā)生的概率,,這個(gè)概率與發(fā)生破壞后造成的損失相乘,得出一個(gè)期望值,。增加安全系數(shù),,破壞的概率降低,破壞損失的期望也隨之降低,,但增加安全系數(shù)會(huì)增加成本,。單就經(jīng)濟(jì)層面而言,因增加安全系數(shù)而增加的成本,,與破壞損失的期望值相等時(shí),,這個(gè)安全系數(shù)是最經(jīng)濟(jì)的,因而也是最合理的,,也可以認(rèn)為,,這就是安全系數(shù)的取值基準(zhǔn)或下限。 |
| 書上說:一般查表,也可以根據(jù)經(jīng)驗(yàn),當(dāng)然既查不到有沒經(jīng)驗(yàn)的,就往和他近似或者受力更復(fù)雜的上面查表或者套經(jīng)驗(yàn). |
| 根據(jù)材料選 |
|
就一大概吧 |
| 一般取值1.5-3,;重要的部位盡量取值大一些,。 |
小黑屋|手機(jī)版|Archiver|機(jī)械社區(qū) ( 京ICP備10217105號(hào)-1,京ICP證050210號(hào),,浙公網(wǎng)安備33038202004372號(hào) )
GMT+8, 2025-2-19 12:48 , Processed in 0.066648 second(s), 16 queries , Gzip On.
Powered by Discuz! X3.4 Licensed
© 2001-2017 Comsenz Inc.